目录
一.排序算法
1.选择排序
1.1原理及图示
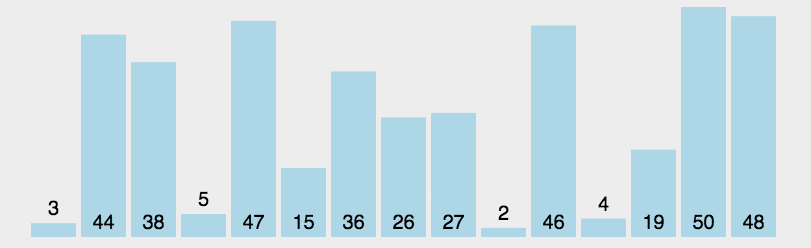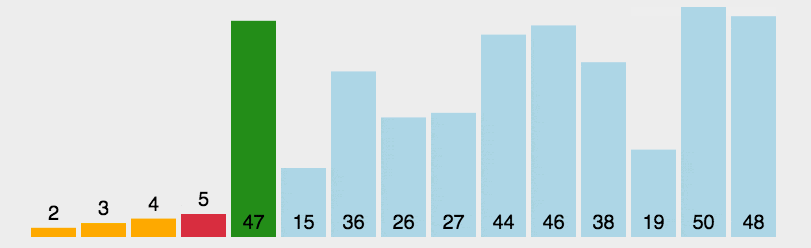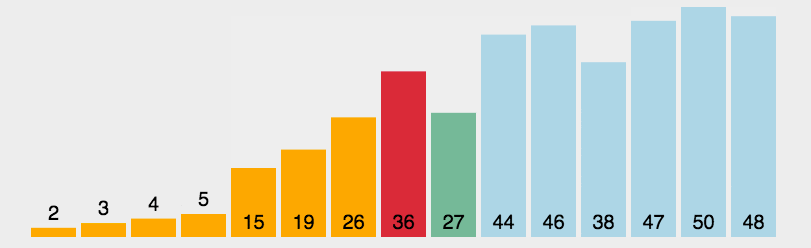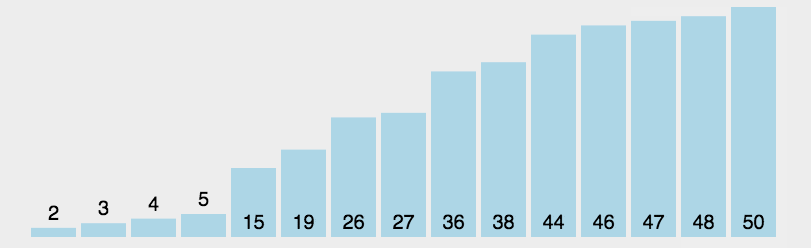
在未排序数组中找到最小(大)关键词元素排在已排序序列初始位置,再如此,将选中的元素插入到已排序序列末尾。(类似于数据结构的进栈操作)
1.2代码部分
#Python代码
def selectionSort(arr):
for i in range(len(arr) - 1):
# 记录最小数的索引
minIndex = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[minIndex]:
minIndex = j
# i 不是最小数时,将 i 和最小数进行交换
if i != minIndex:
arr[i], arr[minIndex] = arr[minIndex], arr[i]
return arr
2.插入排序
2.1原理及图示
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列,依次读取未排序序列中的元素,并插入到已排序序列合理位置。

2.2代码部分
# Python代码
def insertionSort(arr):
for i in range(len(arr)):
preIndex = i-1
current = arr[i]
while preIndex >= 0 and arr[preIndex] > current:
arr[preIndex+1] = arr[preIndex]
preIndex-=1
arr[preIndex+1] = current
return arr
3.归并排序
3.1原理及图示
需要申请内存空间,采用递归函数,依次二分,直至只剩一个元素,再依次合并。(最底层合并是1合1等于2,倒数第二层是2合2=4)

3.2代码部分
# Python代码
def mergeSort(arr):
import math
if(len(arr)<2):
return arr
middle = math.floor(len(arr)/2)
left, right = arr[0:middle], arr[middle:]
return merge(mergeSort(left), mergeSort(right))
def merge(left,right):
result = []
while left and right:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0));
while left:
result.append(left.pop(0))
while right:
result.append(right.pop(0));
return result
4.快速排序
4.1原理及图示
从序列中挑选一个基准值作为分割标准,然后再已分割的两个序列继续分割,再…分割,最后递归地(recursive)合并。如果还不明白请参考更多资料,考试可能要考。

4.2代码部分
#快速排序Python代码
def quickSort(arr, left=None, right=None):
left = 0 if not isinstance(left,(int, float)) else left
right = len(arr)-1 if not isinstance(right,(int, float)) else right
if left < right:
partitionIndex = partition(arr, left, right)
quickSort(arr, left, partitionIndex-1)
quickSort(arr, partitionIndex+1, right)
return arr
def partition(arr, left, right):
pivot = left
index = pivot+1
i = index
while i <= right:
if arr[i] < arr[pivot]:
swap(arr, i, index)
index+=1
i+=1
swap(arr,pivot,index-1)
return index-1
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
5.堆排序
5.1原理及图示
首先构建树结构,随后构建极大(小)堆,然后将最后节点与根节点交换,并将该根节点依次取出。

本次期末考试如无特别说明,高度深度从0开始记。
树的高度为根节点的高度;某节点的高度等于该节点到叶子节点的最长路径(边数);节点的深度是根节点到这个节点所经历的边的个数。 构建极大堆时间复杂度:O(lgn)

5.2代码部分
#堆排序 Python代码
def buildMaxHeap(arr):
import math
for i in range(math.floor(len(arr)/2),-1,-1):
heapify(arr,i)
def heapify(arr, i):
left = 2*i+1
right = 2*i+2
largest = i
if left < arrLen and arr[left] > arr[largest]:
largest = left
if right < arrLen and arr[right] > arr[largest]:
largest = right
if largest != i:
swap(arr, i, largest)
heapify(arr, largest)
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def heapSort(arr):
global arrLen
arrLen = len(arr)
buildMaxHeap(arr)
for i in range(len(arr)-1,0,-1):
swap(arr,0,i)
arrLen -=1
heapify(arr, 0)
return arr
6.计数排序
6.1原理及图示
原理的话看图很好理解;
- (1)找出待排序的数组中最大和最小的元素
- (2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- (3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- (4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1

6.2代码部分
#计数排序Python代码
def countingSort(arr, maxValue):
bucketLen = maxValue+1
bucket = [0]*bucketLen
sortedIndex =0
arrLen = len(arr)
for i in range(arrLen):
if not bucket[arr[i]]:
bucket[arr[i]]=0
bucket[arr[i]]+=1
for j in range(bucketLen):
while bucket[j]>0:
arr[sortedIndex] = j
sortedIndex+=1
bucket[j]-=1
return arr
7.桶排序
桶排序是计数排序的升级版(将离散数值升级为连续区间)。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
- 同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
理想情况:当输入的数据可以均匀的分配到每一个桶中。
最坏情况:所有数据分入一个桶中。
7.1原理及图示
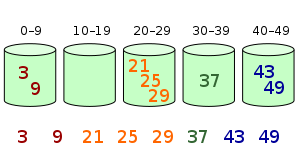
7.2代码部分
#桶排序Python代码
def bucketSort(nums):
#选择一个最大的数
max_num = max(nums)
# 创建一个元素全是0的列表, 当做桶
bucket = [0]*(max_num+1)
# 把所有元素放入桶中, 即把对应元素个数加一
for i in nums:
print(f"{bucket=}")
bucket[i] += 1
# 存储排序好的元素
sort_nums = []
print(f"{bucket=}")
for j in range(len(bucket)):
n = bucket[j]
if n != 0:
for _ in range(n):
print(f"{sort_nums=}{j=}")
sort_nums.append(j)
return sort_nums
nums = [5,6,3,2,1,65,2,0,8,0,9]
print("测试结果:")
print(bucketSort(nums))
8.基数排序
8.1原理及图示
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
- 基数排序 vs 计数排序 vs 桶排序
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;

8.2代码部分
#基数排序Python代码
def radix_sort(s):
"""基数排序"""
i = 0 # 记录当前正在排拿一位,最低位为1
max_num = max(s) # 最大值
j = len(str(max_num)) # 记录最大值的位数
while i < j:
bucket_list =[[] for _ in range(10)] #初始化桶数组
for x in s:
bucket_list[int(x / (10**i)) % 10].append(x) # 找到位置放入桶数组
print(bucket_list)
s.clear()
for x in bucket_list: # 放回原序列
for y in x:
s.append(y)
i += 1
if __name__ == '__main__':
a = [334,5,67,345,7,345345,99,4,23,78,45,1,3453,23424]
radix_sort(a)
print(a)
9.希尔排序
9.1原理及图示
基本思想:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录”基本有序”时,再对全体记录进行依次直接插入排序。
由基本思想可以得出希尔排序也就是升级版的插入排序,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。

9.2代码部分
#Python代码
def shellSort(arr):
import math
gap=1
while(gap < len(arr)/3):
gap = gap*3+1
while gap > 0:
for i in range(gap,len(arr)):
temp = arr[i]
j = i-gap
while j >=0 and arr[j] > temp:
arr[j+gap]=arr[j]
j-=gap
arr[j+gap] = temp
gap = math.floor(gap/3)
return arr
10.排序算法比较
Congretulations! 恭喜你已经复习完了排序算法,下面咱们来比较这些算法吧!
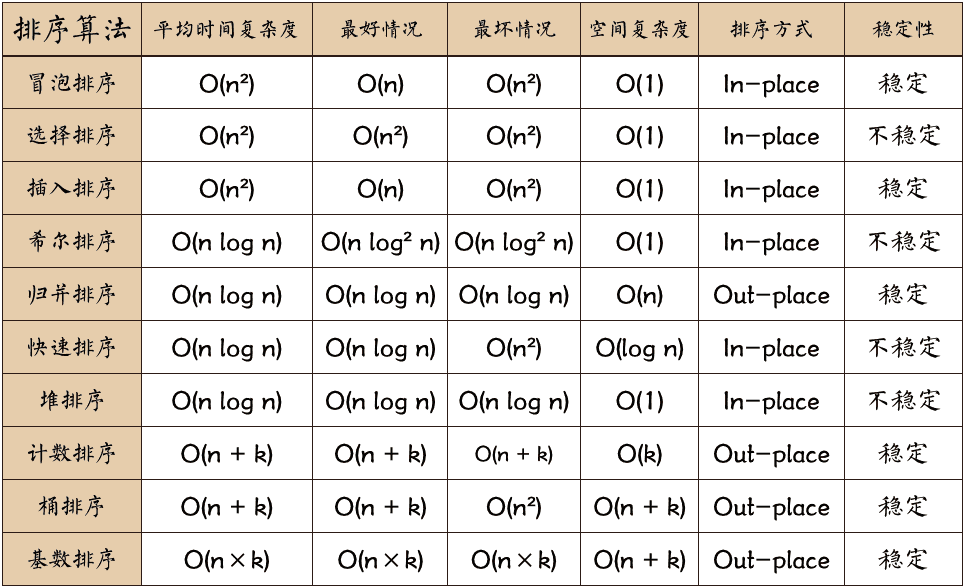
- 稳定性:有随机性的都统一为不稳定,其余为稳定。
- 空间复杂度:精通流程就可以联想到。
- 时间复杂度:需要熟读(伪)代码并了解数学推导
- In-place & Out-place:需不需要开辟辅助空间
二.红黑树
1.红黑树定义和性质
红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质:
- 性质1:每个节点要么是黑色,要么是红色。
- 性质2:根节点是黑色。
- 性质3:每个叶子节点(NIL)是黑色。
- 性质4:每个红色结点的两个子结点一定都是黑色。
- 性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
- 性质5.1:如果一个结点存在黑子结点,那么该结点肯定有两个子结点
一颗简单的红黑树:
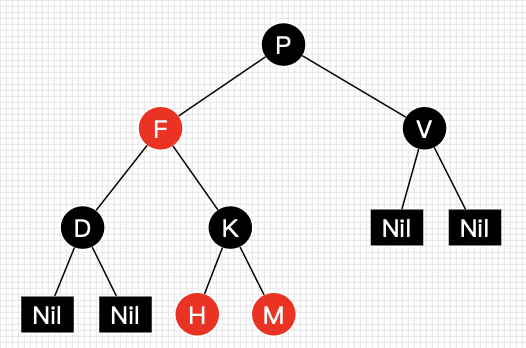
红黑树能自平衡,它靠的是什么?三种操作:左旋、右旋和变色。
- 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。如图3。
- 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
- 变色:结点的颜色由红变黑或由黑变红。
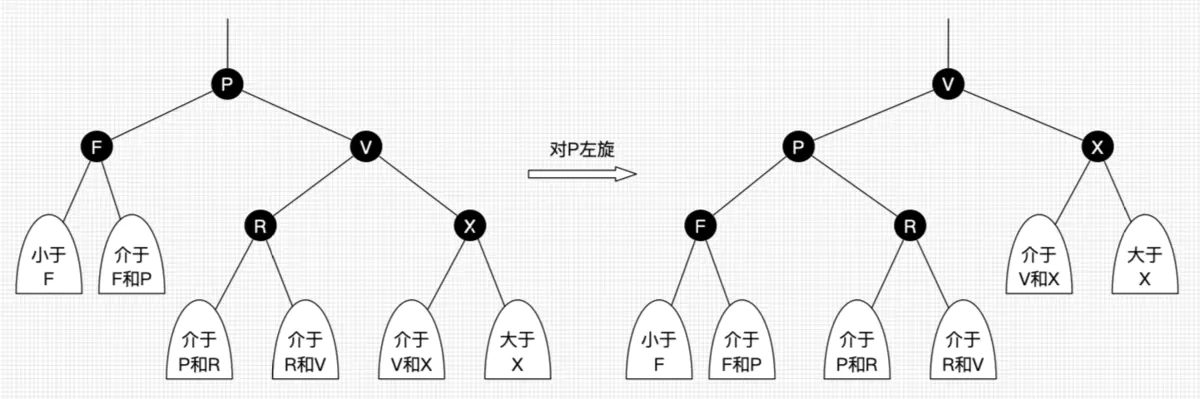
插入和删除相对复杂,需要仔细学习教案和参考资料。
- 插入:插入一共有八种情景;
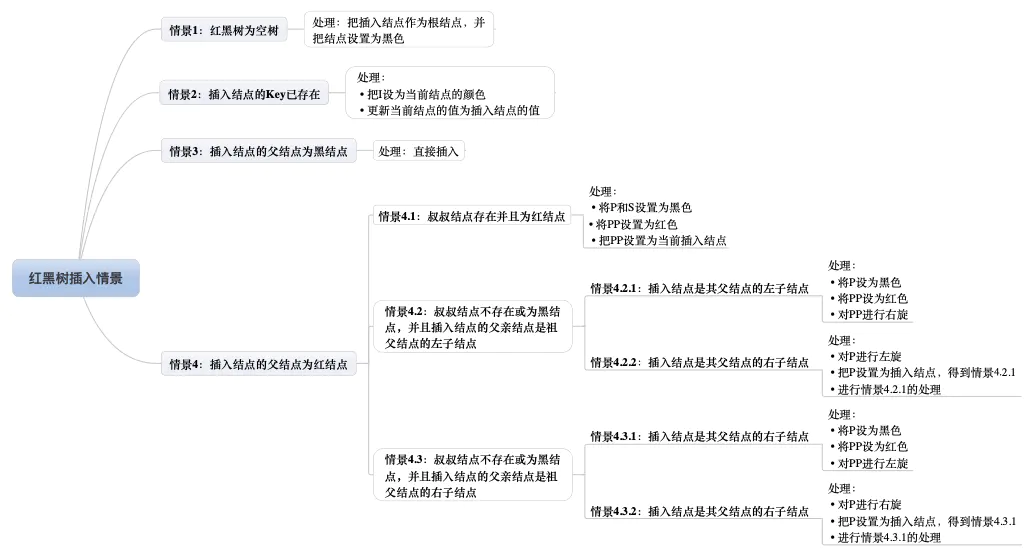
- 删除:删除简化后仍有九种情景。
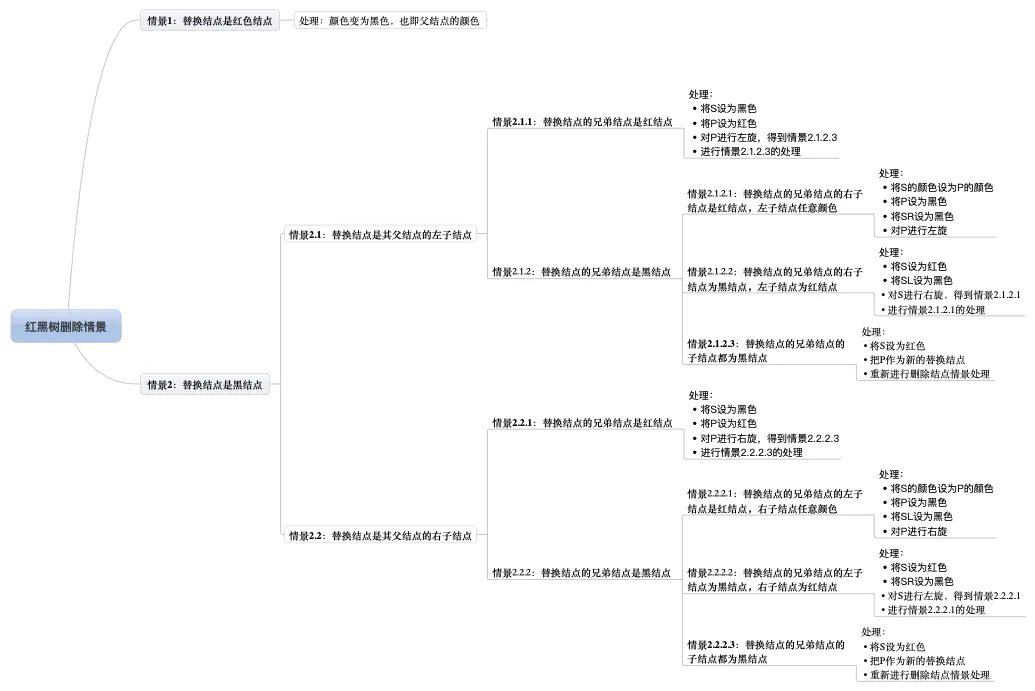
三.动态规划
动态规划三要素:
(1)问题的阶段
(2)每个阶段的状态
(3)相邻两个阶段之间的递推关系
特点:
(1)最优化原理
(2)无后效性
(3)有重叠子问题
关键词:
(1)自底向上
(2)填表法
(3)宁死不用递归
掌握关键:
动态规划不是具体算法,它只是一种思想,要深入理解这种思想。
(1)以大化小,把大问题化成小问题,而小问题的解已经存入在某个数据结构当中了,即可以做到调用。
(2)调用完即可算出当前需算的结果,然后将此结果当做已知,继续向顶进行。
(3)应用:
a.钢条切割问题中,以大化小,比如要算长度d=4的最优价格,先由d=1算起;那么d_4=max(所有已知结果中最优的组合),即遍历操作。
①分成两段,第一段为1,那么第二段为3,而d=3时的最优价格已算出 ,那么①操作就是备选的d_4之一。
②...,第一段为2,那么第二段为2,而d=2时的最优价格也已经算出,那么②操作也是备选d_4之一。
③...,第一段为3,那么第二段为1,而d=3时的最优价格也已经算出,那么③操作也是备选d_4之一。
④...,第一段为4,那么第二段为0,由价格表直接查出价格,也是备选d_4之一。
⑤选出最好的d_4。
b.LCS问题中,采用动态规划的具体思想体现在,他每一步都保存了进度,比如我算出长度为4是因为我发现从长度为3开始有新的可行路径,而不是算每一个长度都从零开始,但依旧是自底向上。我们也可以由此看出,动态规划无论如何怎样变,以此衍生的各种算法不变的只有自底向顶的进行计算操作。
1.钢条切割问题
- ①自顶向下(非多项式级复杂度)
- ②带备忘录的自顶向下(平方阶)
- ③自底向上(平方阶)
①自顶向下
#自顶向下
1 def CutRod(p, n): # 函数返回:切割长度为 n 的钢条所得的最大收益
2 if n == 0:
3 return 0
4 q = -1
5 for i in range(1, n+1):
6 q = max(q, p[i] + CutRod(p, n-i))
7 return q
Core part:Line 5,6.Specific codes go looking up pdf.
②带备忘录的自顶向下
#带备忘录的自顶向下
1 def MemorizedCutRod(p, n):
2 r=[-1]*(n+1) # 数组初始化
3 def MemorizedCutRodAux(p, n, r):
4 if r[n] >= 0:
5 return r[n]
6 q = -1
7 if n == 0:
8 q = 0
9 else:
10 for i in range(1, n + 1):
11 q = max(q, p[i] + MemorizedCutRodAux(p, n - i, r))
12 r[n] = q
13 return q
14 return MemorizedCutRodAux(p, n, r),r
Core part:Line 3,4,5.Specific codes go looking up pdf.
③自底向上
1 def BottomUpCutRod(p, n):
2 r = [0]*(n+1)
3 for i in range(1, n+1):
4 if n == 0:
5 return 0
6 q =0
7 for j in range(1, i+1):
8 q = max(q, p[j]+r[i-j])
9 r[i] = q
10 return r[n],r
Core part:Line All.Specific codes go looking up pdf.
2.矩阵链问题
Python代码
p = [30, 35, 15, 5, 10, 20, 25]
def matrix_chain_order(p):
n = len(p) - 1 # 矩阵个数
m = [[0 for i in range(n)] for j in range(n)]
s = [[0 for i in range(n)] for j in range(n)] # 用来记录最优解的括号位置
for l in range(1, n): # 控制列,从左往右
for i in range(l-1, -1, -1): # 控制行,从下往上
m[i][l] = float('inf') # 保存要填充格子的最优值
for k in range(i, l): # 控制分割点
q = m[i][k] + m[k+1][l] + p[i]*p[k+1]*p[l+1]
if q < m[i][l]:
m[i][l] = q
s[i][l] = k
return m, s
def print_option_parens(s, i, j):
if i == j:
print('A'+str(i+1), end='')
else:
print('(', end='')
print_option_parens(s, i, s[i][j])
print_option_parens(s, s[i][j]+1, j)
print(')', end='')
r, s = matrix_chain_order(p)
print_option_parens(s, 0, 5)
计算次序对计算性能的影响:
假设n=3,A1,A2,A3的维数分别为10×100,100×5,5×50。考察A1×A2×A3需要的数乘次数,有以下
两种计算方式:
(1)(A1×A2)×A3:10×100×5+10×5×50=7500
(2) A1×(A2×A3):100×5×50+10×100×50=75000
通过这个简单的例子足以说明,矩阵的计算次序对计算性能的影响极大。 `①所谓标量乘法就是进行了多少次数与数之间的乘法。` `②矩阵A 的行列数分别为i,j ;矩阵B的行列数分别为k,l,那么要进行矩阵乘法A·B需首先需满足j=k(前列等于后行).` `③我们这边取标量乘法次数为:count=j*k*l.`
其中l为第二个矩阵的列数代表要做几次矩阵乘法(每次矩阵乘法进行了j*k次标量乘法)
④将各数组的行列值分别储存在指定的数据结构中
3.LCS问题
#Python代码
import pandas as pd
def LCS(s1, s2):
size1 = len(s1) + 1
size2 = len(s2) + 1
# 程序多加一行,一列,方便后面代码编写
chess = [[["", 0] for j in list(range(size2))] for i in list(range(size1))]
for i in list(range(1, size1)):
chess[i][0][0] = s1[i - 1]
for j in list(range(1, size2)):
chess[0][j][0] = s2[j - 1]
print("初始化数据:")
display(pd.DataFrame(chess))
for i in list(range(1, size1)): #让第一行和第一列为0
for j in list(range(1, size2)):
if s1[i - 1] == s2[j - 1]: #判断字符是否相等 如果不相等进入下一个判断条件
chess[i][j] = ['↖', chess[i - 1][j - 1][1] + 1]
elif chess[i][j - 1][1] > chess[i - 1][j][1]: #因为初始化为0了,所以自底向上的话:几何上“左边”必然大于"下方",所以置‘←’
chess[i][j] = ['←', chess[i][j - 1][1]]
else:
chess[i][j] = ['↑', chess[i - 1][j][1]]
print("计算结果:")
display(pd.DataFrame(chess))
i = size1 - 1 #从下往上查找
j = size2 - 1
s3 = []
while i > 0 and j > 0:
if chess[i][j][0] == '↖':
s3.append(chess[i][0][0])
i -= 1
j -= 1
if chess[i][j][0] == '←':
j -= 1
if chess[i][j][0] == '↑':
i -= 1
s3.reverse() #逆序输出
print("最长公共子序列:%s" % ''.join(s3))
LCS("abcde", "asdzbd")
# 总之本程序就是由底至顶,由行至列,最后逆序输出。
输出如图,这里使用display函数美观的将其输出(国内技术人员不常用)

要看懂这个图,并且要与上述代码一起看,理解每一步,下面我带大家来理解一下这个图:
1.输入和处理操作本图应从左至右,从上至下看起;输出操作反之。
2.输入:先根据字符串的长度确定矩阵的维度(i+1,j+1),加1的目的是为了实现一种简陋的美观<i class="fas fa-feather-alt"></i>(如果结合pandas可以把这个写在行列索引里),随后将第一行列以各字符顺序填入,其余行列以(flag,0)初始化,其中flag是指↑,↖,←这三种标记。
3.处理:处理操作有两层for循环,显而易见是分别用来控制行列的。先把第一行填满,再把第二行填满....直到最后一行(行数为输入的第一个字符串长度加1),其中每一步都保存上一步的结果,在这个算法中体现在长度上。
从[i,j]=[1,1]看起,根据判断条件,
a.如果s1[i - 1] == s2[j - 1],那么填入[↖,chess[i - 1][j - 1][1] + 1],其中chess[i - 1][j - 1][1] + 1是指矩阵中左上的那一个元素所储存的长度值(储存在第三维度),再加上1
b.如果chess[i][j - 1][1] > chess[i - 1][j][1],即元素chess[i][j]在矩阵中的左边元素大于其正上方的元素,则chess[i][j]就为flag值='←'和原长度,组成的嵌套数组,即chess[i][j] = ['←', chess[i][j - 1][1]]
c.除了上述条件,一切均给chess[i][j]为['↑',原长度]。
d.值得注意的是本处理过程判断条件的先后一定要注意,肯定是先判断第一个if,判断两个子字符是否相等,要不然会乱套。
4.输出,从右下至左上开始读取矩阵元素,最后用reverse函数逆序输出。至于为什么要反着来读,因为这样容易找到"回去"的路。
四.贪心算法
考试资料
- [1] 排序算法选择题
- [2] (李芸老师)算法导论第1次作业
- [3] (李芸老师)算法导论第2次作业
- [4] (李芸老师)算法导论第3次作业
- [5] (李芸老师)2020秋期中测试题
教案
- [1] 算法基础知识
- [2] 函数的增长
- [3] 概率分析与随机算法
- [4] 分治策略
- [5] 堆排序
- [6] 快速排序
- [7] 线性时间排序、统计量
- [8] 基本数据结构
- [9] 二叉搜索树
- [10] 红黑树
- [11] 动态规划
- [12] 贪心算法
- [13] 基本的图算法
- [14] 粒子群优化算法
- [15] 遗传算法与模拟退火算法
参考文献
- [1] 快速排序算法——C/C++
- [2] Python实现二叉树遍历的递归和非递归算法
- [3] 求递归算法时间复杂度:递归树
- [4] 主方法求解递归式
- [5] 30张图带你彻底理解红黑树
- [6] 常见的八大排序算法的比较和选择依据
- [7] 各种排序算法总结和比较
- [8] leetcode410:分割数组的最大值_填表法求解动态规划
温馨提示:用Ctrl+鼠标左键可以创建新窗口打开链接以便流畅体验。
 Clint_chan
Clint_chan 